Genetic Relationship Matrix (GRM)
The genetic relationship matrix (GRM) is the covariance matrix calculated from a set of genetic variants of the individuals. As an important ingredient in mixed models, GRM usually represents the genetic relatedness among individuals. When the entries of the GRM below a specified threshold (usually 0.05) are set to zero, the GRM is transformed into a sparse GRM, which is approximately equivalent to a family kinship matrix.
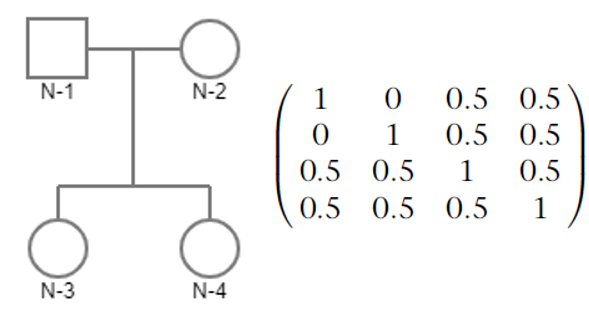
For example, consider a family with four members. The pedigree and the corresponding (sparse) GRM is expected to be:
SPAGRM is a sparse-GRM-based approach to control for sample relatedness. SPAGRM uses the sparse GRM to
- Capture close family relationships.
- Two individuals who have a non-zero element in sparse GRM is assumed in a family, and families are indipedent to each other.
- Estimate precise distributions of genotypes.
- GRM can be used to estimate the variance of genotypes. But it’s limited to estimate more precise distributions of genotypes.
- To understand this, just see the above example. The kinship coefficient (half of the corrsponding element in GRM) for
N-1andN-3is 0.25, and the the kinship coefficient forN-3andN-4is also 0.25. The kinship coefficient for these two pairs are same, but they are genetically different! - Therefore, we introduce identity by descent sharing probabilities, which can exactly describe the genotype distribution between two subjects.
Identity by Descent (IBD)
At a genetic locus, alleles that are inherited copies of a common ancestral allele are said to be identical by descent. The term identical by descent is generally used for referring to recent, rather than ancient, common ancestry. IBD-sharing probabilities are widely used in genetic analyses of samples with related individuals.
Denote $\delta_{ij}^{(0)}$, $\delta_{ij}^{(1)}$, and $\delta_{ij}^{(2)}$ to be the probabilities that two subjects i and j share 0, 1, and 2 alleles identical by decent, respectively, at a locus. $\Phi_{ij}$ is the kinship coefficient for i and j (half of the corrsponding element in GRM). Then the kinship coefficient and IBD-sharing probabilities have the function
\[\Phi_{ij} = 1/2 \times \delta_{ij}^{(2)} + 1/4 \times \delta_{ij}^{(1)}\]To understand this, just see below examples.
N-1andN-3always share one allele in a genetic locus, so that their IBD-sharing probabilities are $\delta_{ij}^{(0)} = 0$, $\delta_{ij}^{(1)} = 1$, and $\delta_{ij}^{(2)} = 0$. The kinship coefficient is $1/2 \times 0 + 1/4 \times 1 = 0.25$.- If genotype of
N-1isAAin one locus, thenN-3must have at least oneAin this locus, regardless of other circumstances. - If genotype of
N-1isaain one locus, thenN-3must have at least oneain this locus, regardless of other circumstances.
- If genotype of
N-3andN-4’s IBD-sharing probabilities are $\delta_{ij}^{(0)} = 0.25$, $\delta_{ij}^{(1)} = 0.5$, and $\delta_{ij}^{(2)} = 0.25$. The kinship coefficient is $1/2 \times 0.25 + 1/4 \times 0.5 = 0.25$.- If genotypes of
N-1andN-2are bothAain one locus, then there is a 0.25 probability that the genotype ofN-3isAA, a 0.5 probability thatN-3isAa, and a 0.25 probability thatN-3isaa, so asN-4. Therefore,N-3andN-4have a 0.25 probability of sharing two alleles, a 0.5 probability of sharing one allele, and a 0.25 probability of sharing no alleles in one locus.
- If genotypes of